로한2의 매력적이면서도 많은 논란을 낳았던 시스템은 바로 <강화>다.
로한2의 <강화>는 파괴가 아닌 다운그레이드 방식으로 얼핏 보면 굉장히 혜자스럽다.
일단 좋은 옵션 무기를 만들면, 이 무기는 파괴될 일이 없고 그 가치를 유지하기 때문이다.
하지만 최근에도 보았듯 여러 강화확률 주작 논란도 있을 뿐더러 강화비용이 대폭 증가했다는 썰이 있다.
그게 사실인지 아닌지는 시스템만이 알 뿐이다.
하지만 이런 말들을 하기에 앞서
적어도 <이번 강화가 운이 좋았는지 안좋았는지> 에 대해서는 판단할 기준이 필요하지 않을까?
평균적으로 강화기대비용이 얼마나 드는지 논리적인 접근으로 수학공식을 통해 구해보자.
1. 문제에 대한 접근
평균 기대 비용 = 1회 강화 비용 X 평균 강화시도 횟수 이다.
1회 강화비용은 고정이니 우리가 구해야할 것은 <평균 강화시도 횟수> 라 할수 있겠다. 이를 수열 a라고 하자.
강화에는 실패 및 1단계하락,2단계하락 등 여러 변수가 존재하기 때문에 일일히 구하는건 애초에 불가능하다.
확률적으로 무한한 경우의수가 있기 때문이다.
하지만 수학에는 <점화식> 이라는 편리한 도구가 있다.
예를 들어 총 10칸의 계단이 있는데 이를 1칸 또는 2칸씩 가는 경우의 수를 구한다고 한다면,
일일히 구한다기보다 10칸까지 가려면 -> 8칸까지 간 경우의수에서 2칸 뛰기 + 9칸까지 간 경우의수에서 1칸뛰기
이 두가지로 나뉘고 결국 모든 계단에서 이 논리가 적용되므로
1번째 계단 = 1가지
2번째 계단 = 1+1 또는 2 로 2가지
3번째 계단 = 2번째 계단 경우 + 3번째 계단 경우 = 1+2 = 3
4번째 계단 = 3번째 계단 경우 + 2번째 계단 경우 = 3 + 2 = 5
5번째 계단 = ... = 5+3 = 8
6번째 = 8+5 = 13
7번째 = 13+ 8 = 21
8번쨰 = 34
9번째 = 55
10번째 = 89
.. 즉 피보나치 수열로 쉽게 구할 수 있다.
2. 실제 문제에 적용
논리를 배웠으니 이를 강화에 적용해보자.
예를 들어 0에서 +10까지 만든다고 하자.
그럼 아래와 같은 식이 나온다.
일단 9강까지 만들고 한번 더 눌러야하므로, [9강까지강화횟수+1]을 적용하고, 성공 실패에 따라 분류하면,
[10강까지 강화 횟수] = [9강까지 강화횟수 + 1]*[10강성공확률] + [9강까지 강화횟수+1+ 10강까지강화횟수 - 8강까지 강화횟수]*[1강떨어질확률] + [9강까지 강화횟수 + 1 + 10강까지 강화횟수 - 7강까지 강화횟수]*[2강 떨어질확률]
이 되겠다.
식이 복잡해보이지만,
첫번째부터 보면, 첫번째는 9->10이 한번에 성공했을때의 기댓값이다.
두번째 항은, 9->10에서 한번 실패해서 8이된다음에 8에서 10까지 갈때의 기댓값이다.
세번째 항은, 9 -> 10에서 한번 실패해서 7이 된다음에 7에서 10까지 갈때의 기댓값이다.
이를 좀더 보기좋게 수식으로 표현하면 아래와 같다.
이를 a10 에 대해 풀면,
이를 모든 경우를 고려해 +(n+1)강까지의 강화로 적용하면,
라는 점화식을 얻을 수 있다.
추가로, +1~+5강까지는 성공률이 100%기 때문에 이 구간의 값은 아래와 같이 알려져있다.
이를통해 a[6]부터 a[25]까지 주어진 확률표를 이용해 풀면,
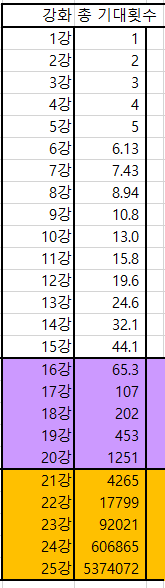
이제 여기에 1회강화비용을 곱해주기만 하면 평균 소모 크론이 나온다.
90제를 기준으로 계산하면 아래와 같다. (물론 90제는 전설이 없지만, 110제를 위해 미리 계산해봤다)
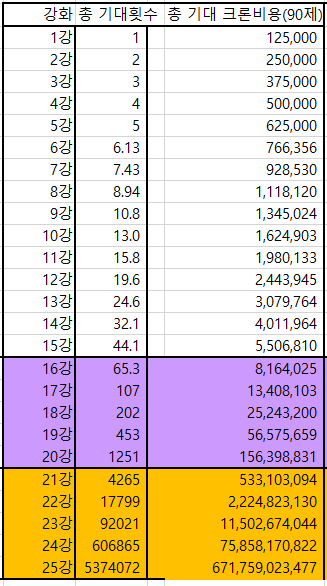
즉 깡 크론으로 강화를 진행했을때, 0 -> 15강은 약 550만크론밖에 안들지만,
0 -> 20강은 1억 5천만 크론정도로 크게 늘어나는 것을 알 수 있다.
보통, 운이 없지만 현실에서 가능한 경우는 평균비용 * 3배 정도 까지이다.
그이상 비용이 들어갔다면, 확률에 문제가 있다고 <의심>은 해볼 수 있다. (물론 아예 불가능한건 아니다)
무튼, 이에 따라 본인이 강화를 진행했을때, 크론을 얼마나 들고서 진행하는게 좋을지 알수있고
또 강화가 끝났을때 내가 운이 좋았는지 안좋았는지에 대한 판독기로 사용할수 있겠다.
최근 개인적인 경험으로는 초반보다 좀 안되는 느낌은 받았지만, 오히려 초반에 성공이 너무 잘 되어 크론소모가 안됐고, 요즘은 평균에 비슷하게 수정됐다는 생각이 든다.
물론, 이 확률의 랜덤성이 코딩마다 완벽하게 기능하는건 아니기에 사람들이 느끼기에
어떤 <특정 연속성공구간> 또는 <특정 연속실패구간>이 있다고 느낄수도 있고, 실제로 있을수도 있다.
하지만 결국 큰수의 법칙에 따라 평균에 회귀하게 된다고 보는 것이 맞을 것이고,
저 구간이 있다한들 그걸 규칙적으로 찾아내는 것은 일반적인 코딩이라면
어렵거나 불가능한 일일 것이다.
3. 식의 응용
마지막으로, 이 수식에 대해 이해하는 분들이라면
이를 잘 이용하여 서버 시세에 따라 "빛나는 상급 강화석"을 몇강에 쓰는게 가장 적절한지도 알 수 있을 것이다.
0/3000
